2022.03.03

差分プライバシーによるテキスト分析のプライバシー保護

はじめまして。株式会社LayerXの恩田と申します。普段はセキュリティ・プライバシー保護技術『Anonify』の開発を行っています。今回はテキスト分析を題材に差分プライバシーを紹介します。

はじめに

個人のプライバシーへの関心の高まり、GDPR違反による巨額の制裁金（企業の全世界年間売上高の2％、または、1,000 万ユーロのいずれか高い方等）が課されることなどの背景から、データ分析に利用されるデータにも十分なプライバシー保護が求められるようになってきています[1]。日本においても令和２年改正個人情報保護法が2022年4月1日に全面施行されます[2]。具体的に改正法[3]では、データ利活用に関する施策の在り方として仮名加工情報が創設されるなど、イノベーション促進のためデータを利活用することと個人のプライバシー配慮の両立が求められています。

しかしながら、「具体的にどのような処置を行えば、プライバシーを保護したことになると言えるのかよく分からない」という方も多いのではないでしょうか。そこで本記事では、プライバシーとして守るべき「要件」の学術的なデファクトスタンダードになっている差分プライバシーを紹介します。学術的にだけではなく実際に利用されている事例を紹介し、差分プライバシーの定義についても簡単に述べます。さらにテキスト分析というユースケースを例に差分プライバシーを適用する実装を行います。実際のコードベースで議論することで、差分プライバシーへの入門ができる記事となればと思います。

差分プライバシーの紹介

差分プライバシーの概要と事例

差分プライバシーは基本的には、パーソナルデータ自体を加工する手法ではなく、統計量や機械学習モデルなど、データに対して処理を行なった結果を保護するものです。差分プライバシーを紹介する前に、まずは単純な統計量を公開することにどのようなプライバシーリスクが存在するのか例を挙げます。

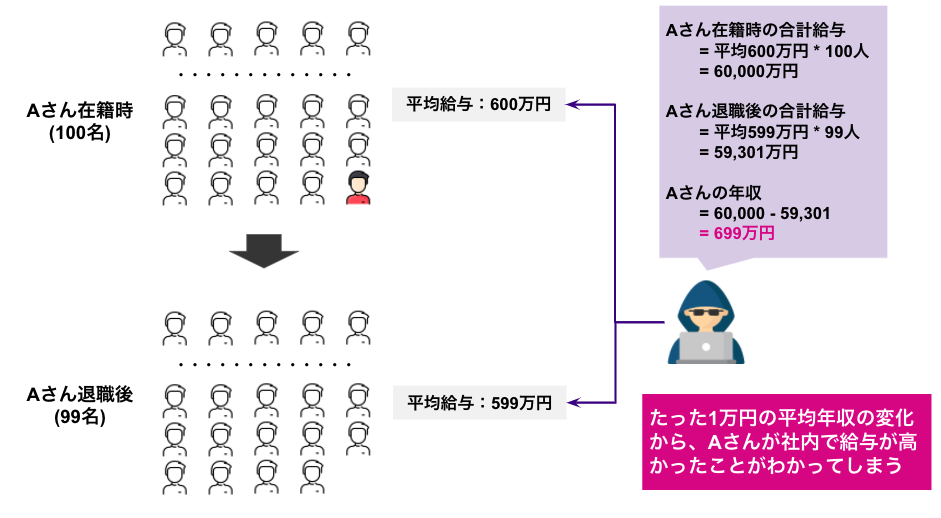
上記の例では、Aさんの年収を知りたい攻撃者が存在し、Aさんが所属している会社は平均年収を統計量として公開している状況を考えています。Aさん在籍時に100名の従業員の平均年収が600万円、Aさん（のみ）が退職した後の平均年収が599万円だとすると、600万円 * 100名 – 599万円 * 99名 = 699万円となり、Aさんの年収が699万円だったことが推定できてしまいます。
このように単純な統計量の公開であっても、パーソナルデータの推定ができてしまうプライバシーリスクが存在します。

このようなリスクへの対策には既に様々な事例があり、その最たる例はアメリカ合衆国国勢調査での差分プライバシーの利用です[4]。アメリカ合衆国国勢調査で公開されるデータには高等教育機関を卒業した人々の所得や学歴、職業に関する内容が含まれます。前述のように統計量の公開は、個人の収入などが露見するリスクを内在しています。この課題を解決するため、アメリカ合衆国国勢調査局は2020年国勢調査において、差分プライバシーを導入しています。差分プライバシーを活用することで国民の匿名性を担保したまま、所得や学歴などの国勢調査結果を全世界に公表しています[5]。
その他にもApple、Meta（旧Facebook）、LinkedIn、Microsoftなども、差分プライバシーを活用したサービスやプロダクトを提供しています[6]。

差分プライバシー入門

差分プライバシーは、Dworkら（2006）によって機密データに基づく統計データの公表に対して数学的に証明可能なプライバシー保証を提供するアプローチとして考案されました [7]。また2017年には、コンピュータサイエンス分野の最高峰である「ゲーデル賞」を受賞しています[8]。

具体的なプライバシー保証の方法としては、機密データに基づく統計データに、プライバシーを保護するノイズを注入します。このノイズによって、統計的有用性を維持したまま、統計データにおける数学的に証明可能なプライバシー保証を提供します。

より正確には、特定の個人が含まれているか・含まれていないのかをクエリの出力の結果から区別しにくくするメカニズムを適用します。この区別のしにくさをプライバシーパラメタ $ \epsilon $ で抑えます。定義としては、メカニズム$ \mathcal{M} $が$ \epsilon $-差分プライバシーであるとは、任意の$ \mathcal{S} \subseteq \mathrm{Range(\mathcal{M})} $と、レコードが一つだけ異なるような隣接データベース$ D, D’ $に対して、式 $ \eqref{def_dp} $が成り立つことです。

$$ \frac{\mathrm{Pr} [\mathcal{M}(D) \in \mathcal{S}]}{\mathrm{Pr} [\mathcal{M}(D’) \in \mathcal{S}]} \leq e^{\epsilon} \label{def_dp} \tag{1} $$

式 $ \eqref{def_dp} $ は、特定の個人が含まれるデータセット $ D $ と、含まれないデータセット $ D’ $ それぞれについて、メカニズムを適用した出力が条件 $ S $ を満たす確率の比が $ e^{\epsilon} $ で抑えられている、と解釈できます。仮に全く区別できない場合は $ \mathrm{Pr} [\mathcal{M}(D) \in \mathcal{S}] = \mathrm{Pr} [\mathcal{M}(D’) \in \mathcal{S}] $ となるので、その比は$ 1 $（= $e^0 $）になります。逆に区別が容易になればなるほど確率の比は大きくなり、その度合いが $ e^{\epsilon} $ として定量化されています。

また式 $ \eqref{def_dp} $ を満たすことを$ \epsilon $-差分プライバシーを満たすといいますが、 任意の 隣接データセット $ D, D’ $ に対して成立することを述べており、特定の時点でのデータセット $ D, D’ $ だけでなく、将来も含めあり得るすべてのデータセット $ D, D’ $ に対して定義されます。つまり差分プライバシーはメカニズム $ \mathcal{M} $ に対しての性質であり、 特定の データセットに対しての定義でないことに注意してください。

代表的なメカニズムとしてLaplaceメカニズムがあります。Laplaceメカニズムはその名の通りクエリの出力に対してLaplace分布に基づくノイズを付与することで差分プライバシーを実現します。通常、平均 $ 0 $ のLaplace分布を用いるので以下のようなノイズを加えることになります。

$$ \mathrm{Lap}(x; b) = \frac{1}{2b} \exp \bigl( – \frac{|x|}{b} \bigr) \label{laplace} \tag{2} $$

ここで $ b $ はスケールパラメータであり、 $ b $ が大きくなると、大きなノイズが加わる確率が高くなります。 $ b = \Delta f / \epsilon $ とすることで、$ \epsilon $-差分プライバシーを満たすことが証明されています[9]。

なお $ \Delta f $ はクエリ $ f $ の（ $ l_1 $-）sensitivityで、以下のように定義されます。

$$ \Delta f = \underset{\underset{||D-D’||_1 = 1}{D, D’}}{\max} ||\mathcal{M}(D) – \mathcal{M}(D’) ||_1 \label{def_sensitivity} \tag{3} $$

sensitivityはクエリ出力がデータセット$ D $ と $ D’ $において最大でどの程度変化するか、その最大値を表します。特定個人が含まれているかどうかによってクエリ出力が大きく変化する場合には、その大きさに応じてより大きなノイズを加えなければならないことを示しています。

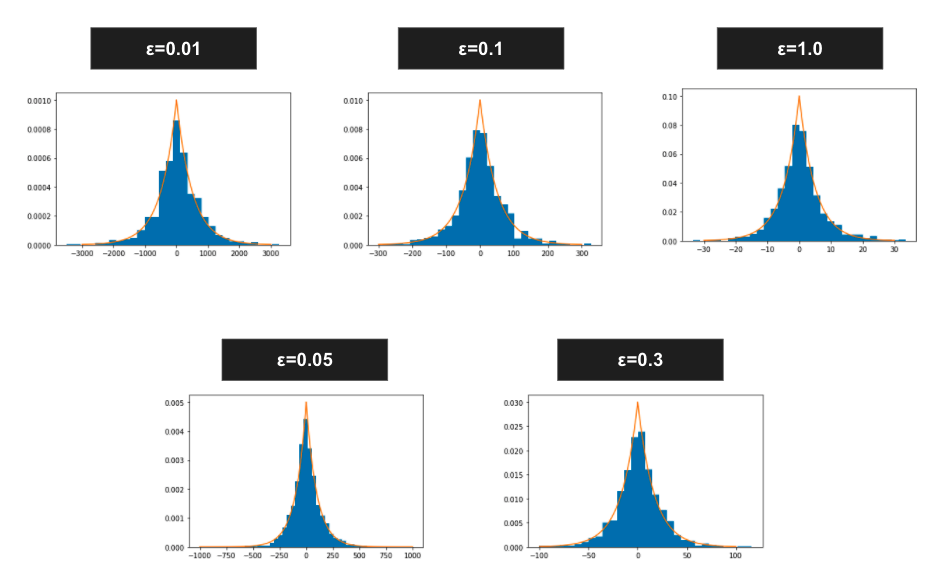
また $ \epsilon $ は先述したプライバシーパラメタであり、より小さい $ \epsilon $ はより大きなノイズを加えることになります。 $ \Delta f = 5 $ で固定した場合（後述するテキスト分析の例で設定する値に合わせています）に、 $ \epsilon $ を変化させるとどのくらいのノイズを加えることになるかを示したものが以下図になります。$ \epsilon $ とノイズの大きさの目安にしていただければと思います。

差分プライバシーを用いたテキスト分析

さて差分プライバシーの概要を掴んだところで、実際に差分プライバシーを適用したテキスト分析を行ってみたいと思います。今回は株式会社リクルートが運営する旅行サイト『じゃらんnet』のクチコミデータ[10]を用いてテキスト分析を行います。公開されているデータのクチコミ部分のみを抽出し、重複を排除した全40,145件を対象とします。クチコミの具体例をいくつか挙げます。

部屋は狭かったですが、寝るだけなので十分でした。
従業員さんの対応もよくお部屋もきれいでした。
大浴場が狭く脱衣場が不衛生だった。
居酒屋、コンビニはタクシーでないと行けません。
今回は広めのタイプCを利用しましたが、ロールカーテン下の隙間が大きい為(3cm程度かな?
冷蔵庫があったら嬉しかったなぁ
セキュリティーもしっかりしているので安心でした。
コーヒーすら薄くて美味しくない......
値段が安く温泉なので、またの機会があったら宿泊したいと思います。

部屋は狭かったですが、寝るだけなので十分でした。

従業員さんの対応もよくお部屋もきれいでした。

大浴場が狭く脱衣場が不衛生だった。

居酒屋、コンビニはタクシーでないと行けません。

今回は広めのタイプCを利用しましたが、ロールカーテン下の隙間が大きい為(3cm程度かな?

冷蔵庫があったら嬉しかったなぁ

セキュリティーもしっかりしているので安心でした。

コーヒーすら薄くて美味しくない......

値段が安く温泉なので、またの機会があったら宿泊したいと思います。

このようなクチコミに対して、筆者が主観的にクチコミの感情をpositive・negative・neutralでアノテーションを行いました。アノテーションの割合としては以下のようになりました。

表1 各アノテーションの割合

sentiment	割合[%]
positive	85.02
negative	10.06
neutral	4.92

本記事で扱うテキスト分析のストーリーとして、以下の分析ケース①と分析ケースケース②を考えます。

分析ケース①は上記でアノテーションを付与したクチコミに対して、positive・negative・neutralなクチコミで登場頻度の高い上位単語を対象とします。
このケースでは、各単語の出現頻度に対してLaplaceノイズを加え、差分プライバシー保護を実現します。出現頻度にノイズが加わるため、上位単語の順位が変化することが想定されるので、プライバシーパラメタ $ \epsilon $ と上位単語の順位変化の関係に着目します。

そして分析ケース②では機械学習アルゴリズムへの差分プライバシー適用を考えます。
具体的にはpositiveなクチコミを投稿したユーザは「リピートする」、negative・neutralなクチコミを投稿したユーザは「リピートしない」と仮定し、クチコミからリピートする・しないを予測する分類問題を解きます。今回は差分プライバシー保護されたナイーブベイズとロジスティック回帰の2つの機械学習モデルを用いて、プライバシーパラメタ $ \epsilon $ の変化に対して分類の精度がどのように変化するかを確認します。

以下では分析ケース①②をコードベースで実装していきます。なお今回の分析で用いるサンプルコードは、Google Colaboratory上で動作を確認しています。

分析ケース①: 記述統計へのDP適用

テキスト分析にあたり、各クチコミに対してspaCy[11]とGiNZA[12]を用いて形態素解析を実施します。GiNZAはpipでインストールすることができます。

!pip install ja-ginza

1 2	!pip install ja-ginza

アノテーション済みのクチコミをcsvファイルから読み込みます。

import pandas as pd
data_path = &quot;&lt;YOUR&gt;/&lt;PATH&gt;/&lt;TO&gt;/reviews.csv&quot;
df = pd.read_csv(data_path)
df

import pandas as pd

data_path = "<YOUR>/<PATH>/<TO>/reviews.csv"

df = pd.read_csv(data_path)

読み込み後のDataFrameは以下のようになっています。

まずは特徴量として、クチコミをBag-of-Words（以下BoW）として表現します。この際、クチコミを形態素解析し、クチコミの特徴を表す単語を調べるため特定の品詞（具体的には形容詞・副詞・間投詞・名詞・固有名詞・動詞）を抽出しました。また同一クチコミ内で同じ単語が重複されていた場合は、一つの単語として重複を排しています。さらにクチコミの文書ベクトルと類似度の高い上位5単語（ MAX_TERMS_IN_DOC = 5 で設定可能です）を、そのクチコミの代表単語とすることとしています。

from sklearn.feature_extraction.text import CountVectorizer
import itertools
import spacy
from typing import List, Tuple
nlp = spacy.load('ja_ginza')
POS = ['ADJ', 'ADV', 'INTJ', 'PROPN', 'NOUN', 'VERB']
MAX_TERMS_IN_DOC = 5
NGRAM=1
MAX_DF=1.0
MIN_DF=0.0
NUM_VOCAB=10000
def flatten(*lists) -&gt; list:
  res = []
  for l in list(itertools.chain.from_iterable(lists)):
    for e in l:
      res.append(e)
  return res
def remove_duplicates(l: List[Tuple[str, float]]) -&gt; List[Tuple[str, float]]:
  d = {}
  for e in l:
    d[e[0]] = e[1]
  return list(d.items())
df[&quot;doc&quot;] = [nlp(review) for review in df[&quot;review&quot;]]
bows = {}
cvs = {}
for sentiment in df[&quot;sentiment&quot;].unique():
  tokens = []
  for doc in df[df[&quot;sentiment&quot;] == sentiment][&quot;doc&quot;]:
    similarities = [(token.similarity(doc), token.lemma_) for token in doc if token.pos_ in POS]
    similarities = remove_duplicates(similarities)
    similarities = sorted(similarities, key=lambda sim: sim[1], reverse=True)[:MAX_TERMS_IN_DOC]
    tokens.append([similaritity[1] for similaritity in similarities])
  cv = CountVectorizer(ngram_range=(1,NGRAM), max_df=MAX_DF, min_df=MIN_DF, max_features=NUM_VOCAB)
  bows[sentiment] = cv.fit_transform(flatten(tokens)).toarray()
  cvs[sentiment] = cv

from sklearn.feature_extraction.text import CountVectorizer

import itertools

import spacy

from typing import List, Tuple

nlp = spacy.load('ja_ginza')

POS = ['ADJ', 'ADV', 'INTJ', 'PROPN', 'NOUN', 'VERB']

MAX_TERMS_IN_DOC = 5

NGRAM=1

MAX_DF=1.0

MIN_DF=0.0

NUM_VOCAB=10000

def flatten(*lists) -> list:

res = []

for l in list(itertools.chain.from_iterable(lists)):

for e in l:

res.append(e)

return res

def remove_duplicates(l: List[Tuple[str, float]]) -> List[Tuple[str, float]]:

d = {}

for e in l:

d[e[0]] = e[1]

return list(d.items())

df["doc"] = [nlp(review) for review in df["review"]]

bows = {}

cvs = {}

for sentiment in df["sentiment"].unique():

tokens = []

for doc in df[df["sentiment"] == sentiment]["doc"]:

similarities = [(token.similarity(doc), token.lemma_) for token in doc if token.pos_ in POS]

similarities = remove_duplicates(similarities)

similarities = sorted(similarities, key=lambda sim: sim[1], reverse=True)[:MAX_TERMS_IN_DOC]

tokens.append([similaritity[1] for similaritity in similarities])

cv = CountVectorizer(ngram_range=(1,NGRAM), max_df=MAX_DF, min_df=MIN_DF, max_features=NUM_VOCAB)

bows[sentiment] = cv.fit_transform(flatten(tokens)).toarray()

cvs[sentiment] = cv

差分プライバシーなしでの単語の登場頻度

まずは差分プライバシーの保護を行わず、真の登場頻度（回数）を算出してみましょう。アノテーションを行ったpositive・neutral・negativeごとに単語の登場頻度をカウントします。ここでは上位20単語（ TOP_K = 20 で設定可能です）を計算するコードなっていますが、結果は見やすさを優先し上位5単語のみとしています。

TOP_K = 20
vocabs = {}
term_fequencies = {}
for sentiment in df[&quot;sentiment&quot;].unique():
  bow = bows[sentiment]
  cv = cvs[sentiment]
  vocab  = cv.vocabulary_
  term_fequency = np.sum(bow, axis=0)
  vocabs[sentiment] = vocab
  term_fequencies[sentiment] = term_fequency
  indices_topk = np.argsort(term_fequency)[::-1][:TOP_K]
  bow_topk = np.take(bow, indices_topk, axis=1)
  reverse_vocab = { vocab[k]:k for k in vocab.keys() }
  words = [reverse_vocab[i] for i in indices_topk]
  print(sentiment, &quot;:&quot;)
  for w, c in zip(words, term_fequency[indices_topk]):
    print(w, &quot;:&quot;, c)

TOP_K = 20

vocabs = {}

term_fequencies = {}

for sentiment in df["sentiment"].unique():

bow = bows[sentiment]

cv = cvs[sentiment]

vocab = cv.vocabulary_

term_fequency = np.sum(bow, axis=0)

vocabs[sentiment] = vocab

term_fequencies[sentiment] = term_fequency

indices_topk = np.argsort(term_fequency)[::-1][:TOP_K]

bow_topk = np.take(bow, indices_topk, axis=1)

reverse_vocab = { vocab[k]:k for k in vocab.keys() }

words = [reverse_vocab[i] for i in indices_topk]

print(sentiment, ":")

for w, c in zip(words, term_fequency[indices_topk]):

print(w, ":", c)

positive・neutral・negativeごとの上位5単語とその登場頻度は以下のようになりました。

表2 positiveの上位5単語と登場頻度

rank	word	count
1	普通	366
2	部屋	262
3	利用	244
4	朝食	207
5	十分	203

表3 neutralの上位5単語と登場頻度

rank	word	count
1	良い	4749
2	部屋	3133
3	美味しい	2705
4	朝食	2610
5	満足	2060

表4 negativeの上位5単語と登場頻度

rank	word	count
1	部屋	501
2	残念	359
3	狭い	346
4	少し	288
5	風呂	261

全体の85%のクチコミがpositiveにあたるため、登場頻度としてpositiveが一つ桁の大きい結果となりました。また部屋 はpositive・neutral・negativeのいずれでもよく使われる単語のようです。各クラスの違いに着目した指標に変更することは考えられますが、本記事では差分プライバシー保護を行ったときにこの単語頻度がどのように変化するかを捉えることを主目的としているため、別の特徴量に切り替えることはせず、上記結果に対して差分プライバシーを適用していきます。

差分プライバシーで保護を行った単語の登場頻度

差分プライバシーのライブラリとしてはGoogleの差分プライバシープロジェクトのPython実装であるPyDP[13]を利用します。こちらもpipでインストールします。

pip install python-dp

1 2	pip install python-dp

PyDPにはカウントクエリにLaplaceメカニズムを組み込んだCountクラスがありますが、集計前の元のデータをリストとして入力する必要があるので、便宜的に以下のpreprocess_for_private_counts関数を定義します。この関数はpydpのCountを使うためにindexをリピートさせたリストを作る関数です。具体例としては以下のような動作となっています。

例1
input: [1, 1, 1]
output: [[0], [1], [2]]
例2
input: [3, 1, 4]
output: [[0, 0, 0], [1], [2, 2, 2, 2]]

例1

input: [1, 1, 1]

output: [[0], [1], [2]]

例2

input: [3, 1, 4]

output: [[0, 0, 0], [1], [2, 2, 2, 2]]

例2の場合でいえば、単語_{index=0}が3つあることを考えると理解しやすいかと思います。

from pydp.algorithms.laplacian import Count
import numpy as np
def preprocess_for_private_counts(tf: np.ndarray) -&gt; List[np.ndarray]:
  repeated_words = []
  for i, term in enumerate(tf):
    repeated_words.append(np.repeat(i, term))
  return repeated_words

from pydp.algorithms.laplacian import Count

import numpy as np

def preprocess_for_private_counts(tf: np.ndarray) -> List[np.ndarray]:

repeated_words = []

for i, term in enumerate(tf):

repeated_words.append(np.repeat(i, term))

return repeated_words

登場頻度にLapaceノイズを加えることで差分プライバシー保護を適用する実装は以下のとおりです。今回はプライバシーパラメタ $ \epsilon $ を $ [0.1, 10] $ で変化させており、各 $ \epsilon $ について、一回だけ登場頻度をカウントします。

import numpy as np
from typing import List, Tuple
from pydp.algorithms.laplacian import Count
def cal_private_count(
    epsilon: float,
    max_partition_contributed: float,
    max_contributions_per_partition: float,
    repeated_words: List[np.ndarray],
  ) -&gt; List[int]:
  private_counts = []
  for repeated_word in repeated_words:
    counter = Count(epsilon, max_partition_contributed, max_contributions_per_partition)
    count = counter.quick_result(repeated_word)
    private_counts.append(count)
  return private_counts
def top_k_words_and_counts(k: int, tf: np.ndarray, vocab: dict) -&gt; List[Tuple[str, int]]:
  indices_topk = np.argsort(tf)[::-1][:k]
  reverse_vocab = { vocab[key]:key for key in vocab.keys() }
  words = [reverse_vocab[i] for i in indices_topk]
  counts = [tf[i] for i in indices_topk]
  return list(zip(words, counts))
epsilons = [0.01, 0.05, 0.1, 0.3, 0.7, 1.0, 2.0, 3.0, 7.0, 10.0]
MAX_DUPLICATED_TERMS = 1
for eps in epsilons:
  print(&quot;ε: &quot;, eps)
  for sentiment in df[&quot;sentiment&quot;].unique():
    repeated_words = preprocess_for_private_counts(term_fequencies[sentiment])
    private_counts = cal_private_count(eps, MAX_TERMS_IN_DOC, MAX_DUPLICATED_TERMS, repeated_words)
    words_and_counts = top_k_words_and_counts(TOP_K, private_counts, vocabs[sentiment])
    print(sentiment, &quot;:&quot;, words_and_counts)

import numpy as np

from typing import List, Tuple

from pydp.algorithms.laplacian import Count

def cal_private_count(

epsilon: float,

max_partition_contributed: float,

max_contributions_per_partition: float,

repeated_words: List[np.ndarray],

) -> List[int]:

private_counts = []

for repeated_word in repeated_words:

counter = Count(epsilon, max_partition_contributed, max_contributions_per_partition)

count = counter.quick_result(repeated_word)

private_counts.append(count)

return private_counts

def top_k_words_and_counts(k: int, tf: np.ndarray, vocab: dict) -> List[Tuple[str, int]]:

indices_topk = np.argsort(tf)[::-1][:k]

reverse_vocab = { vocab[key]:key for key in vocab.keys() }

words = [reverse_vocab[i] for i in indices_topk]

counts = [tf[i] for i in indices_topk]

return list(zip(words, counts))

epsilons = [0.01, 0.05, 0.1, 0.3, 0.7, 1.0, 2.0, 3.0, 7.0, 10.0]

MAX_DUPLICATED_TERMS = 1

for eps in epsilons:

print("ε: ", eps)

for sentiment in df["sentiment"].unique():

repeated_words = preprocess_for_private_counts(term_fequencies[sentiment])

private_counts = cal_private_count(eps, MAX_TERMS_IN_DOC, MAX_DUPLICATED_TERMS, repeated_words)

words_and_counts = top_k_words_and_counts(TOP_K, private_counts, vocabs[sentiment])

print(sentiment, ":", words_and_counts)

差分プライバシーなしのときと同様にpositive・neutral・negativeごとの上位5単語とその登場頻度を表にまとめます。ここで登場頻度は真の値ではなく、Laplaceメカニズムによってノイズが加わった値であることに注意してください。上位5単語のみを表にまとめているため、count列には正の値しかありませんが、大きな負のノイズが加わった結果、負の値となることもあります。また、真の値が 0 （一度も登場しない単語）であっても、ノイズが加わった結果、正の値となることもあります。

表5 positiveの上位5単語と登場頻度（DP保護なし・あり）

	no DP		ε=0.01		ε=0.05		ε=0.1		ε=0.3		ε=0.7		ε=1.0
rank	word	count	word	count	word	count	word	count	word	count	word	count	word	count
1	良い	4749	良い	5330	良い	4733	良い	4746	良い	4735	良い	4740	良い	4754
2	部屋	3133	ソコソコ	3778	部屋	3257	部屋	3153	部屋	3105	部屋	3135	部屋	3128
3	美味しい	2705	階段	3213	朝食	2542	美味しい	2699	美味しい	2710	美味しい	2700	美味しい	2716
4	朝食	2610	朝食	3178	美味しい	2387	朝食	2625	朝食	2618	朝食	2610	朝食	2607
5	満足	2060	心身	3171	満足	2031	満足	2049	満足	2021	満足	2059	満足	2052

表6 neutralの上位5単語と登場頻度（DP保護なし・あり）

	no DP		ε=0.01		ε=0.05		ε=0.1		ε=0.3		ε=0.7		ε=1.0
rank	word	count	word	count	word	count	word	count	word	count	word	count	word	count
1	普通	366	ネット	3102	深い	578	普通	342	普通	406	普通	371	普通	372
2	部屋	262	友達	3069	最小限	567	利用	338	部屋	257	部屋	264	部屋	264
3	利用	244	ホテル	2650	関係	553	ハンガー	335	利用	243	利用	241	利用	239
4	朝食	207	まず	2470	普通	518	十分	298	十分	199	朝食	228	十分	204
5	十分	203	デザート	2174	レベル	498	できる	274	朝食	195	十分	205	朝食	204

表7 negativeの上位5単語と登場頻度（DP保護なし・あり）

	no DP		ε=0.01		ε=0.05		ε=0.1		ε=0.3		ε=0.7		ε=1.0
rank	word	count	word	count	word	count	word	count	word	count	word	count	word	count
1	部屋	501	持参	3227	混む	726	部屋	500	部屋	467	部屋	513	部屋	486
2	残念	359	勿体	3005	買い	704	残念	454	残念	358	残念	367	残念	342
3	狭い	346	物凄い	2809	だし	604	通す	412	狭い	347	狭い	343	狭い	341
4	少し	288	入れる	2703	なし	582	狭い	384	少し	307	少し	299	少し	290
5	風呂	261	水垢	2665	少し	526	夏休み	290	風呂	256	風呂	264	風呂	256

no DP と記載した列が、差分プライバシー保護がされていない状態での単語と登場頻度になっています。それより右の列がプライバシーパラメタ $ \epsilon $ を変化させたときの単語と登場頻度です。
positiveの1位である「良い」に着目すると、どの $ \epsilon $ に対しても1位を維持できていることがわかります。一方でneutralでは真の1位は「普通」で366回ですが、 $ \epsilon = 0.01 $ において「ネット」が1位になっています。さらにその回数は3,102となっており、大きなノイズが加わった結果、1位に押し上げられたものだと理解できます。ノイズはLaplace分布に従っているので、理論的には $ [ – \infty, \infty ] $の大きさのノイズが加わりますが、今回の結果から数千オーダーの単語数に対しては $ \epsilon \geq 0.1 $ 、数百オーダーの単語数に対しては $ \epsilon \geq 0.3 $ であれば差分プライバシー保護がない結果と大きく有用性は劣化しないことがわかります。

より定量的に評価するため、$ \epsilon $ を変化させたときに、上位k単語がどの程度維持されるのかを差分プライバシー保護をしていない上位k単語との一致率で比較します。例えば、上位5単語が {良い, 部屋, 美味しい, 朝食, 満足} だったとき、ノイズを加わった結果 {良い, ソコソコ, 階段, 朝食, 心身} となった場合は5単語中2単語が元の上位5単語と一致しているため、一致率は40%となります。また実際のテキスト分析において上位k単語を求めるケースでは、どのような単語が登場するかに興味があり、必ずしも厳密な順位が必要でないこともあると想定し、k単語中の一致率では順序を考慮していません。また今回の結果はLaplaceメカニズムを一度だけ適用した結果であることに注意してください。

まず、negativeとneutralの結果は以下のようになりました。 $ \epsilon $ は0.1〜10で検証していますが、$ \epsilon > 3$ では飽和しているので図上は省略しています。

図4 negativeにおける元上位単語との一致率

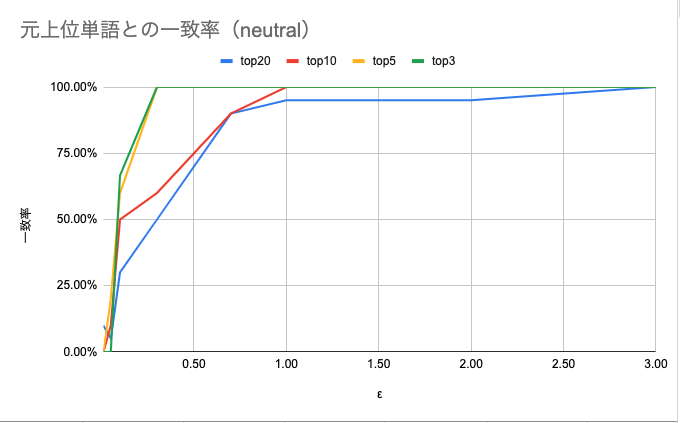
図5 neutralにおける元上位単語との一致率

$ \epsilon \geq 1 $ では上位3, 5, 10, 20のいずれでも一致率がほぼ100%になっていることがわかります。 $ \epsilon < 1 $ においては、上位k単語のkが大きくなるほど緩やかに上昇しています。逆にいうと上位3単語のように元から上位にいた単語ほど上位に居続けることがわかります。

一方、negativeの上位20単語の $ \epsilon = 2 $ では一致率が100%から落ちています。これは元々21位以下だった単語（今回は「朝食付き」が該当しました）に大きなノイズが加わった結果、上位20位に入ってきたためです。この順位の入れ替えは登場頻度の差が僅差であるほど起きやすいことにも注意してください。

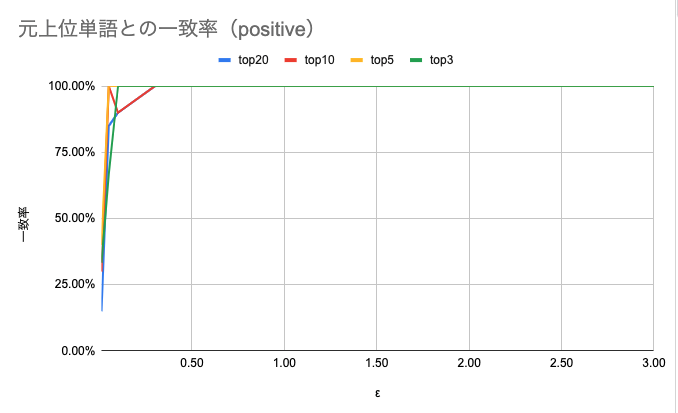
図6 positiveにおける元上位単語との一致率

こちらはpositiveに関する一致率の結果です。上位単語が数千オーダーであるpositiveはnegative・neutralに対して桁が一つ大きい登場頻度でした。positiveの一致率はnegative・neutralに対して急峻に100%の一致率に到達する結果となっており、より小さな $ \epsilon $ であっても高い有用性を保てることを示しています。

分析ケース②: MLアルゴリズムへの差分プライバシー適用

差分プライバシーのライブラリとしてはIBMが開発しているdiffprivlib[14]を利用します。diffprivlibでは種々の機械学習アルゴリズムに対して差分プライバシーを組み込んでおり、今回はナイーブベイズとロジスティック回帰を使って差分プライバシーで保護された分類問題を解きます。

ナイーブベイズ

概要

まずはナイーブベイズを用いて、クチコミからリピートする・しないを分類します。diffprivlibのナイーブベイズはIEEE/WIC ACM International Joint Conferences on Web Intelligence 2013で発表された論文[15]を元に実装されています。ナイーブベイスの学習は、カテゴリカルな属性に対しては、特徴量を $ x_k $、分類するクラスを $ c_j $として、 $ P(x_k | c_j) = \frac{n_{kj}}{n} $ のように学習します。ここで $ n $ はトレーニングセットのサイズ、 $ n_{kj} $ はクラスが$ c_j $ かつ特徴量が$ x_k $ となるトレーニングセットのサイズです。つまるところ各クラスのカウントを算出しているので分析ケース①と同じように差分プライバシーのメカニズムを適用することができます。数値変数に対しては、ガウス分布に従うことを仮定した上でその平均と分散のsensitivityを考え、差分プライバシーが適用されます。詳細については論文[15]で議論されていますので、興味がある方はご参照ください。

差分プライバシーなしのナイーブベイズによる分類

ナイーブベイズの分類でも 分析ケース①: 記述統計へのDP適用 で作成したBoWを特徴量とします。各変数については 分析ケース①: 記述統計へのDP適用 と同様のためコードは省略します。ただし、sentimentは予測するラベルにあたるため、sentimentごとにBoW化せずに、すべてのクチコミをまとめてBoW化します。以下ではBoW化の実装からコードベースで記載します。

from sklearn.feature_extraction.text import CountVectorizer
import itertools
import numpy as np
import spacy
from typing import List, Tuple
POS = ['ADJ', 'ADV', 'INTJ', 'PROPN', 'NOUN', 'VERB']
MAX_TERMS_IN_DOC = 5
NGRAM=1
MAX_DF=1.0
MIN_DF=0.01
NUM_VOCAB=10000
def flatten(*lists) -&gt; list:
  res = []
  for l in list(itertools.chain.from_iterable(lists)):
    for e in l:
      res.append(e)
  return res
def remove_duplicates(l: List[Tuple[str, float]]) -&gt; List[Tuple[str, float]]:
  d = {}
  for e in l:
    d[e[0]] = e[1]
  return list(d.items())
tokens = []
for doc in df[&quot;doc&quot;]:
  similarities = [(token.similarity(doc), token.lemma_) for token in doc if token.pos_ in POS]
  similarities = remove_duplicates(similarities)
  similarities = sorted(similarities, key=lambda sim: sim[1], reverse=True)[:MAX_TERMS_IN_DOC]
  tokens.append([similaritity[1] for similaritity in similarities])
cv = CountVectorizer(ngram_range=(1,NGRAM), max_df=MAX_DF, min_df=MIN_DF, max_features=NUM_VOCAB)
bow = cv.fit_transform([&quot; &quot;.join(ts) for ts in tokens]).toarray()

from sklearn.feature_extraction.text import CountVectorizer

import itertools

import numpy as np

import spacy

from typing import List, Tuple

POS = ['ADJ', 'ADV', 'INTJ', 'PROPN', 'NOUN', 'VERB']

MAX_TERMS_IN_DOC = 5

NGRAM=1

MAX_DF=1.0

MIN_DF=0.01

NUM_VOCAB=10000

def flatten(*lists) -> list:

res = []

for l in list(itertools.chain.from_iterable(lists)):

for e in l:

res.append(e)

return res

def remove_duplicates(l: List[Tuple[str, float]]) -> List[Tuple[str, float]]:

d = {}

for e in l:

d[e[0]] = e[1]

return list(d.items())

tokens = []

for doc in df["doc"]:

similarities = [(token.similarity(doc), token.lemma_) for token in doc if token.pos_ in POS]

similarities = remove_duplicates(similarities)

similarities = sorted(similarities, key=lambda sim: sim[1], reverse=True)[:MAX_TERMS_IN_DOC]

tokens.append([similaritity[1] for similaritity in similarities])

cv = CountVectorizer(ngram_range=(1,NGRAM), max_df=MAX_DF, min_df=MIN_DF, max_features=NUM_VOCAB)

bow = cv.fit_transform([" ".join(ts) for ts in tokens]).toarray()

今回はクチコミによりリピートする・しないを分類タスクとするため、positiveなクチコミを投稿したユーザはクチコミをする、neutralとnegativeなクチコミを投稿したユーザはクチコミをしないと仮定します。さらにクチコミする・しないに 1 と 0 のラベルを再付与しています。また、作成した特徴量を学習用のデータセットと、分類用のデータセットに分割します。今回は test_size=0.2 としました。

from sklearn import datasets
from sklearn.model_selection import train_test_split
m = {
    &quot;positive&quot;: 1,
    &quot;neutral&quot;: 0,
    &quot;negative&quot;: 0,
}
df[&quot;sentiment&quot;] = df[&quot;sentiment&quot;].map(m)
df[&quot;bow&quot;] = bow.tolist()
X_train, X_test, y_train, y_test = train_test_split(df[&quot;bow&quot;], df[&quot;sentiment&quot;], test_size=0.2)
X_train = [list(x) for x in X_train.to_numpy()]
X_test = [list(x) for x in X_test.to_numpy()]

from sklearn import datasets

from sklearn.model_selection import train_test_split

m = {

"positive": 1,

"neutral": 0,

"negative": 0,

}

df["sentiment"] = df["sentiment"].map(m)

df["bow"] = bow.tolist()

X_train, X_test, y_train, y_test = train_test_split(df["bow"], df["sentiment"], test_size=0.2)

X_train = [list(x) for x in X_train.to_numpy()]

X_test = [list(x) for x in X_test.to_numpy()]

sklearnを用いてナイーブベイズによる分類を実行します。

from sklearn.naive_bayes import GaussianNB
clf = GaussianNB()
clf.fit(X_train, y_train.to_numpy())
print(&quot;accuracy: &quot;, clf.score(X_test, y_test.to_numpy()))

from sklearn.naive_bayes import GaussianNB

clf = GaussianNB()

clf.fit(X_train, y_train.to_numpy())

print("accuracy: ", clf.score(X_test, y_test.to_numpy()))

差分プライバシー保護なしのaccuracyは 69.66 % となりました。

差分プライバシーありのナイーブベイズによる分類

さて続いて差分プライバシーが組み込まれたナイーブベイズによる分類を実施します。プライバシーパラメタ $ \epsilon $ は $ [10^{-2}, 10^2] $の範囲を対数スケールで50分割し、accuracyを計算します。差分プライバシーを適用すると実行ごとに異なるノイズが加わるため、各 $ \epsilon $ に対して20回ずつaccuracyを算出し、accuracyのばらつきを計算できるようにしています。またsensitivityを決定するためのパラメタとして bounds を設定する必要がありますが、今回は同一クチコミ内で使われた同一単語の重複を排除しているため、一つのクチコミによって各次元（ある単語の登場回数）は高々1しか変化しません。そこで np.zeros と np.ones を bounds としています。

import numpy as np
import matplotlib.pyplot as plt
from diffprivlib.models import GaussianNB
epsilons = np.logspace(-2, 2, 50)
dim = np.array(X_train).shape[1]
lowers = np.zeros(dim)
uppers = np.ones(dim)
accuracies = {}
for epsilon in epsilons:
  accuracy = []
  for i in range(20):
    clf = GaussianNB(bounds=(lowers, uppers), epsilon=epsilon)
    clf.fit(X_train, y_train.to_numpy())
    accuracy.append(clf.score(X_test, y_test.to_numpy()))
  accuracies[epsilon] = accuracy

import numpy as np

import matplotlib.pyplot as plt

from diffprivlib.models import GaussianNB

epsilons = np.logspace(-2, 2, 50)

dim = np.array(X_train).shape[1]

lowers = np.zeros(dim)

uppers = np.ones(dim)

accuracies = {}

for epsilon in epsilons:

accuracy = []

for i in range(20):

clf = GaussianNB(bounds=(lowers, uppers), epsilon=epsilon)

clf.fit(X_train, y_train.to_numpy())

accuracy.append(clf.score(X_test, y_test.to_numpy()))

accuracies[epsilon] = accuracy

結果をグラフに描画してみましょう。エラーバーは標準偏差になっています。

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd
plt.style.use('default')
sns.set()
sns.set_style('whitegrid')
sns.set_palette('gray')
x = epsilons
y = []
e = []
for key in accuracies.keys():
  y.append(np.mean(accuracies[key]))
  e.append(np.std(accuracies[key]))
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.semilogx(x, y)
ax.errorbar(x, y, yerr=e, marker='o', capthick=1, capsize=10, lw=1)
ax.set_xlabel(&quot;epsilon&quot;)
ax.set_ylabel(&quot;accuracy&quot;)
ax.set_ylim(0, 1)
plt.show()

import matplotlib.pyplot as plt

import seaborn as sns

import numpy as np

import pandas as pd

plt.style.use('default')

sns.set()

sns.set_style('whitegrid')

sns.set_palette('gray')

x = epsilons

y = []

e = []

for key in accuracies.keys():

y.append(np.mean(accuracies[key]))

e.append(np.std(accuracies[key]))

fig = plt.figure()

ax = fig.add_subplot(1, 1, 1)

ax.semilogx(x, y)

ax.errorbar(x, y, yerr=e, marker='o', capthick=1, capsize=10, lw=1)

ax.set_xlabel("epsilon")

ax.set_ylabel("accuracy")

ax.set_ylim(0, 1)

plt.show()

出力は以下のようになりました。

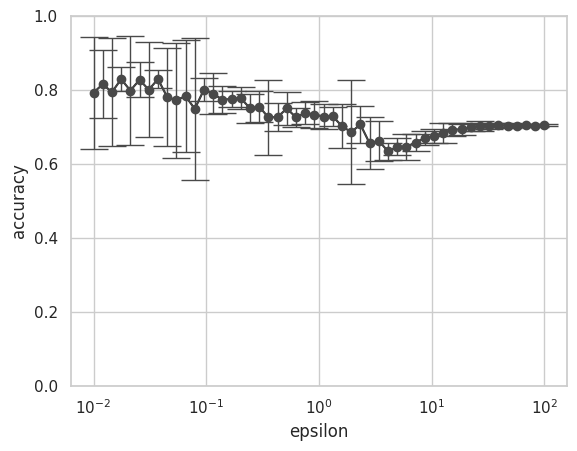
図7 ナイーブベイズにおけるεとaccuracyの関係

小さい $ \epsilon $ に対してはaccuracyの分散が大きく、 $ \epsilon $ が大きくなるにつれてこの分散が小さくなっていることがわかります。小さな $ \epsilon $ では加わるノイズも大きくなるため、分類において元々の特徴（今回ではsentimentごとに特徴づけられたBoW）よりもノイズの影響が大きくなったためだと考えられます。また差分プライバシー保護なしのaccuracyが 69.66 % だったことを踏まえると、$ \epsilon $ が十分大きければ（$ \epsilon \geq 10 $）、差分プライバシー保護なしのaccuracyに収束していくことも図からわかります。

ロジスティック回帰

概要

diffprivlibで実装されている差分プライバシー版のロジスティック回帰は、Journal of Machine Learning Research 2011で発表された論文[16]が元になっています。機械学習アルゴリズム一般へ差分プライバシーを組み込む方法には、大きく出力摂動法と目的関数摂動法の2種類が存在します[9]。差分プライバシーの定義に戻ると、特定レコードが含まれるデータセット $ D $と含まれないデータセット $ D’ $ に対してのクエリ出力にメカニズムを適用した結果が $ \mathcal{M}(D) $ と $ \mathcal{M}(D’) $ となるの確率の比が$ e^{\epsilon} $で抑えられていることでした。機械学習アルゴリズムを重み $ w $ を求めるクエリと捉えると、この重みにLaplaceノイズなどの摂動を加えることは自然な考え方でしょう。この方式が出力摂動法です。
一方、目的関数摂動法では、その名の通り目的関数に摂動（ノイズ）を加えます。例えば経験的損失に正則化項を加えた目的関数があるとすれば、この目的関数にLaplaceノイズを加えるといった方式です。diffprivlibのロジスティック回帰では目的関数摂動法が使われています。

差分プライバシーなしのロジスティック回帰による分類

特徴量を学習用のデータセットと、分類用のデータセットに分割するところまではナイーブベイズのコードと同一のため省略します。ロジスティック回帰においてもsklearnを用いて差分プライバシーのないaccuracyを計算します。

from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(random_state=0).fit(X_train, y_train.to_numpy())
print(&quot;accuracy: &quot;, clf.score(X_test, y_test.to_numpy()))

from sklearn.linear_model import LogisticRegression

clf = LogisticRegression(random_state=0).fit(X_train, y_train.to_numpy())

print("accuracy: ", clf.score(X_test, y_test.to_numpy()))

差分プライバシー保護なしのaccuracyは 86.84 % となりました。

差分プライバシーありのロジスティック回帰回帰による分類

続いて差分プライバシーが組み込まれたロジスティック回帰による分類を実施します。ナイーブベイズにおける bounds に相当するパラメタとして data_norm が存在します。今回はBoWの次元数（= 単語数）のl2ノルムを採用しました。ナイーブベイズの際と同様にプライバシーパラメタ $ \epsilon $ は $ [10^{-2}, 10^2] $の範囲を対数スケールで50分割し、各 $ \epsilon $ に対して20回ずつaccuracyを算出します。

import math
import numpy as np
import matplotlib.pyplot as plt
from diffprivlib.models import LogisticRegression
epsilons = np.logspace(-2, 2, 50)
dim = np.array(X_train).shape[1]
data_norm = math.sqrt(dim)
accuracies = {}
for epsilon in epsilons:
  accuracy = []
  for i in range(20):
    clf = LogisticRegression(data_norm=data_norm, epsilon=epsilon).fit(X_train, y_train.to_numpy())
    accuracy.append(clf.score(X_test, y_test.to_numpy()))
  accuracies[epsilon] = accuracy

import math

import numpy as np

import matplotlib.pyplot as plt

from diffprivlib.models import LogisticRegression

epsilons = np.logspace(-2, 2, 50)

dim = np.array(X_train).shape[1]

data_norm = math.sqrt(dim)

accuracies = {}

for epsilon in epsilons:

accuracy = []

for i in range(20):

clf = LogisticRegression(data_norm=data_norm, epsilon=epsilon).fit(X_train, y_train.to_numpy())

accuracy.append(clf.score(X_test, y_test.to_numpy()))

accuracies[epsilon] = accuracy

結果をグラフに描画しました（描画のコードはナイーブベイズのときと同一です）。

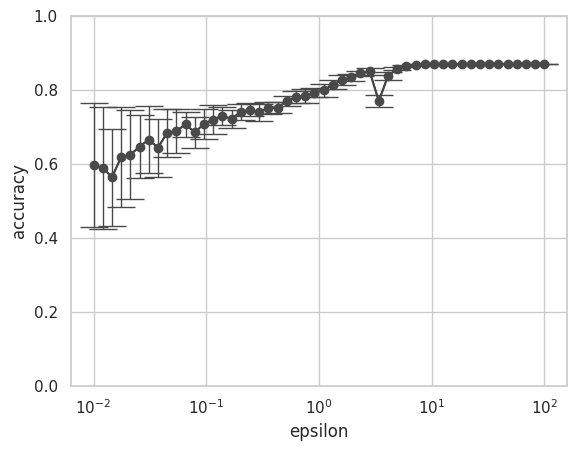
case2_logi_result

図8 ロジスティック回帰におけるεとaccuracyの関係

ロジスティック回帰の結果も、小さい $ \epsilon $ に対してはaccuracyの分散が大きく、 $ \epsilon $ が大きくなると分散が小さくなる結果となりました。また差分プライバシー保護なしのaccuracyが 86.84 % だったことから、 $ \epsilon $ が十分大きければ（$ \epsilon \geq 10 $）、差分プライバシー保護なしのaccuracyに収束するという結果も同様でした。

また分析ケース①では $ \epsilon $ が 0.1〜0.3である程度の有用性を保てていましたが、今回の分析ケース②では $ \epsilon \geq 10 $ で安定したaccuracyとなる結果でした。

終わりに

本記事では、差分プライバシーの概要と定義、分析ケースとして単語の登場頻度、ナイーブベイズ、ロジスティック回帰を実際のコードベースで紹介しました。今回紹介したdiffprivlibには差分プライバシーが組み込まれたrandom forest、k-means、linear regression、PCAが利用可能です。本記事の応用として他モデルを試してみることも興味深いかと思います。
また実際に差分プライバシーを適用するにあたっては、具体的に $ \epsilon $ の値をいくつにするかを設計する必要があります。その設計には深いドメインへの理解が求められますが、適切なプライバシー保証のもとデータ分析ができるようになり、事業で取れる選択肢にも広がりが出てきます。これらは応用的な内容になってきますが、本記事では実際にテキストの分析業務を行われている方にも馴染み深いケースに対して差分プライバシーを適用する例を紹介させて頂いたことが、少しでも差分プライバシーを理解する助けになっていれば幸いです。

References

[1] 日本貿易振興機構（ジェトロ）ブリュッセル事務所海外調査部欧州ロシア CIS 課, 「EU 一般データ保護規則（GDPR）」に関わる実務ハンドブック（入門編）, 2016年11月. https://www.jetro.go.jp/ext_images/_Reports/01/dcfcebc8265a8943/20160084.pdf
[2] 個人情報保護委員会, 令和２年改正個人情報保護法について, 2022年2月13日アクセス. https://www.ppc.go.jp/personalinfo/legal/kaiseihogohou/
[3] 個人情報保護委員会, 個人情報の保護に関する法律等の一部を改正する法律（概要）, 2020年6月, 2022年2月13日アクセス. https://www.ppc.go.jp/files/pdf/200612_gaiyou.pdf
[4] Andrew David Foote, Ashwin Machanavajjhala, Kevin McKinney, Releasing Earnings Distributions using Differential Privacy, Disclosure Avoidance System For Post-Secondary Employment Outcomes (PSEO), JOrivacy Confidentiality, 2019, 2022年2月13日アクセス. https://journalprivacyconfidentiality.org/index.php/jpc/article/view/722
[5] United States Census Bereau, Census Bureau Sets Key Parameters to Protect Privacy in 2020 Census Results, 2021, 2022年2月13日アクセス. https://www.census.gov/newsroom/press-releases/2021/2020-census-key-parameters.html
[6] Damien Desfontaines, A list of real-world uses of differential privacy, 2021, 2022年2月13日アクセス. https://desfontain.es/privacy/real-world-differential-privacy.html
[7] Dwork, C., McSherry, F., Nissim, K., & Smith, A. Calibrating noise to sensitivity in private data analysis. Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 3876 LNCS, 265–284. 2006. https://doi.org/10.1007/11681878_14
[8] European Association for Theoretical Computer Science, 2017 Gödel Prize, 2017, 2022年2月13日アクセス. https://www.eatcs.org/index.php/component/content/article/1-news/2450-2017-godel-prize
[9] 佐久間淳, データ解析におけるプライバシー保護, 機械学習プロフェッショナルシリーズ, 講談社, 2016.
[10] 株式会社リクルート, リクルートのAI研究機関、『じゃらんnet』のクチコミを活用した日本語自然言語処理の発展を加速する学術研究用データセットを公開, 2020, 2022年2月13日アクセス. https://www.recruit.co.jp/newsroom/2020/1019_18866.html
[11] E. Jones, T. Oliphant, P. Peterson, et al. SciPy: Open source scienti?c tools for Python. 2001–. http://www.scipy.org/
[12] megagonlabs, GiNZA – Japanese NLP Library, 2019-. https://megagonlabs.github.io/ginza/
[13] chinmays99, Python API for Google’s Differential Privacy library, OpenMined, 2020-. https://pypi.org/project/python-dp/
[14] IBM, Diffprivlib: The IBM Differential Privacy Library, 2019-. https://github.com/IBM/differential-privacy-library
[15] Vaidya, Jaideep, et al. "Differentially private naive bayes classification." 2013 IEEE/WIC/ACM International Joint Conferences on Web Intelligence (WI) and Intelligent Agent Technologies (IAT). Vol. 1. IEEE, 2013. https://www.researchgate.net/publication/262254729_Differentially_Private_Naive_Bayes_Classification
[16] Chaudhuri, Kamalika, Claire Monteleoni, and Anand D. Sarwate. "Differentially private empirical risk minimization." Journal of Machine Learning Research 12.3 2011. https://www.jmlr.org/papers/volume12/chaudhuri11a/chaudhuri11a.pdf

Recruit Tech Blog

タグから見つける

タグから見つける

職種を選択

事業領域を選択

差分プライバシーによるテキスト分析のプライバシー保護

はじめに

差分プライバシーの紹介

差分プライバシーの概要と事例

差分プライバシー入門

差分プライバシーを用いたテキスト分析

分析ケース①: 記述統計へのDP適用

差分プライバシーなしでの単語の登場頻度

差分プライバシーで保護を行った単語の登場頻度

分析ケース②: MLアルゴリズムへの差分プライバシー適用

ナイーブベイズ

概要

差分プライバシーなしのナイーブベイズによる分類

差分プライバシーありのナイーブベイズによる分類

ロジスティック回帰

概要

差分プライバシーなしのロジスティック回帰による分類

差分プライバシーありのロジスティック回帰回帰による分類

終わりに

References